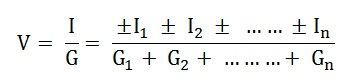El teorema o principio de Millman (llamado así en honor al electrónico ruso Jacob Millman) es utilizado para obtener directamente la diferencia de potencial entre los extremos de un circuito eléctrico. Resulta indicado cuando se tiene sólo dos nodos, o lo que es lo mismo, varias ramas en paralelo.

En concreto, establece que:

Esto mismo, formalmente:

V m = F 1 R 1 F 2 R 2 F 3 R 3 . . . F n R n 1 R 1 1 R 2 1 R 3 . . . 1 R n = ∑ k = 1 N F k . G k ∑ k = 1 N G k = ∑ k = 1 N F k R k ∑ k = 1 N 1 R k {\displaystyle V_{m}={{{{F_{1}} \over {R_{1}}} {{F_{2}} \over {R_{2}}} {{F_{3}} \over {R_{3}}} ... {{F_{n}} \over {R_{n}}}} \over {{1 \over {R_{1}}} {1 \over {R_{2}}} {1 \over {R_{3}}} ... {1 \over {R_{n}}}}}={\frac {\sum _{k=1}^{N}F_{k}.G_{k}}{\sum _{k=1}^{N}G_{k}}}={\frac {\sum _{k=1}^{N}{\frac {F_{k}}{R_{k}}}}{\sum _{k=1}^{N}{\frac {1}{R_{k}}}}}}

Donde F es la fuente de tensión o de corriente según sea el caso y G, es la conductancia.

Observación: Para propósitos del cálculo, el valor de la fuente de tensión o de corriente es igual a cero en una rama que consiste en nada más que una resistencia.

Demostración del Principio de Millman

Considerando el esquema del circuito que aparece en la figura:

Como las ramas (Zk; Ek) están en paralelo, se trabaja con las admitancias Y k = 1 Z k {\displaystyle Y_{k}={\frac {1}{Z_{k}}}} y las transformaciones Thévenin -> Norton : I N k = E k ⋅ Y k {\displaystyle IN_{k}=E_{k}\cdot Y_{k}} (convención generador)

Para cada rama (fuente de tensión e impedancia), se obtiene, a partir de la Ley de Ohm: I k = Y k ⋅ ( V m − E k ) {\displaystyle I_{k}=Y_{k}\cdot (V_{m}-E_{k})}

A continuación, a partir de la Ley de Kirchhoff, tenemos:

∑ k = 1 N I k = 0 {\displaystyle \sum _{k=1}^{N}I_{k}=0}

∑ k = 1 N Y k ⋅ ( V m − E k ) = 0 {\displaystyle \sum _{k=1}^{N}Y_{k}\cdot (V_{m}-E_{k})=0}

Y desarrollando...

∑ k = 1 N Y k ⋅ V m = ∑ k = 1 N Y k ⋅ E k {\displaystyle \sum _{k=1}^{N}Y_{k}\cdot V_{m}=\sum _{k=1}^{N}Y_{k}\cdot E_{k}}

V m = ∑ k = 1 N E k ⋅ Y k ∑ k = 1 N Y k = ∑ k = 1 N E k Z k ∑ k = 1 N 1 Z k {\displaystyle V_{m}={\frac {\sum _{k=1}^{N}E_{k}\cdot Y_{k}}{\sum _{k=1}^{N}Y_{k}}}={\frac {\sum _{k=1}^{N}{\frac {E_{k}}{Z_{k}}}}{\sum _{k=1}^{N}{\frac {1}{Z_{k}}}}}}

Normas prácticas para aplicar Millman

  • Se señalan dos nodos A y B, por ejemplo la parte superior e inferior.
  • Se asigna un sentido arbitrario a la tensión Vab, si el resultado final es positivo, la polaridad adoptada es cierta, si es negativo hay que cambiar la polaridad.
  • Se calculan las corrientes parciales de cada una de las ramas producidas por los generadores de cada rama actuando independientemente. Si una rama no tiene generadores, se supone la corriente de esa rama igual a cero.
  • Las corrientes parciales que se dirigen hacia el nodo que se ha considerado positivo se toman con el signo . Las corrientes que se alejan se consideran -.
  • La tensión total Vab viene dada por la expresión general:

V a b = ∑ I ∑ 1 R {\displaystyle V_{ab}={\frac {\sum I}{\sum {\frac {1}{R}}}}}

(donde 1 R {\displaystyle {\frac {1}{R}}} se conoce también como conductancia)


Ejemplo práctico

V A B = − 30 V 10 Ω 1 Ω − 50 V 6 Ω 4 Ω 0 1 10 Ω 1 Ω 1 6 Ω 4 Ω 1 8 Ω = − 24.46 V {\displaystyle V_{AB}={\frac {-{\frac {30V}{10\Omega 1\Omega }}-{\frac {50V}{6\Omega 4\Omega }} {0}}{{\frac {1}{10\Omega 1\Omega }} {\frac {1}{6\Omega 4\Omega }} {\frac {1}{8\Omega }}}}=-24.46V}

El signo - indica que la polaridad real de la tensión va de B( ) a A(-) por lo que VBA = 24.46V.

Véase también

  • Redes eléctricas
  • Leyes de Kirchhoff
  • Principio de Thévenin
  • Principio de Maxwell
  • Principio de Norton

Teorema de Millman 2023

Teorema o Principio de Millman Mi Universo Electrónico PDF

Teorema de Millman UNIGAL

teorema de millman by on Prezi

El teorema de Millman La fisica y quimica